3. Poincaré és Lorentz csoport, O(1,1), O(1,3)

Tér és idő a klasszikus fizikában

A fizikában nagyon fontos szerepet játszik a Lorentz csoport. Ez írja le a tér-, és az idő-koordináták transzformációját két egymáshoz képest egyenletes sebességgel mozgó megfigyelő között.

Képzeljük el, amint Iluska egyhelyben ül, Jancsi pedig v sebességgel egyenletesen szalad. Iluska úgy választja a koordináta-rendszerét, hogy abban ő ül az origóban, Jancsi pedig az első tengely mentén szalad, pozitív irányban. Jancsi szemszögéből nézve persze minden éppen fordítva van: Ő is magát helyezi az origóba (a saját koordináta-rendszerében), Iluska és az erdő fái pedig mozognak, az első koordináta tengely mentén, negatív iráyban. Az időt is mérik mindketten, attól a pillanattól kezdve, amikor elváltak. Fontos észrevétel, hogy az időt mindketten egyformán mérik. Galilei tanulmányozta az egyenletes mozgást, és azt találta, hogy az a pont, amit Iluska (x,y,z) Iluska koordinátával illet, az Jancsi szerint az (x−vt,y,z) Jancsi koordinátákat kapja. Hasonló képlet kapható akkor is, ha Jancsi sebességét a (v x,v y,v z) vektor írja le. Ezt a transzformációt: (x,y,z)→(x−v xt,y−v yt,z−v zt) Galilei transzformációnak nevezzük. Ennek a transzformációs szabálynak van egy nagyon fontos következménye: a sebesség additivitása. Ez azt jelenti, hogy ha Jancsi v sebeséggel szalad Iluskához képest, és Peti w sebességgel halad Jancsihoz képest, akkor Peti sebessége v+w lesz Iluskához képest.

Tér és idő a relativitás elméletben

Nagyon nagy sebességek esetén azonban gyökeresen más a helyzet. Tudjuk, hogy a fény sebessége nem léphető át, sőt, a fény minden rendszerből nézve ugyanakkora sebességűnek látszik. Ez pedig szöges ellentétben áll a sebesség additivitásával, tehát Galilei transzformációs képleteivel is. Alaposabb vizsgálattal az is kiderül, hogy az idővel is baj van: nem lehetséges olyan transzformációt találni, amelyben Iluska és Jancsi számára egyformán telik az idő. Tehát külön tér és idő helyett egy négy dimenziós téridővel fogunk dolgozni:

/1. Konvenció: A téridő pontjai a világtörténelem eseményei, ezeket koordinátázhatjuk ( 1 idő- és 3 tér-koordinátával). Emberek, tárgyak életútja, vagy más szóval világvonala (azaz az általuk átélt események összessége) a téridőben folytonos vonalat alkot, amelynek a sebessége mindenütt kisebb a fénysebességnél.

Az inercia rendszer fogalma még Galileitől származik: Ő precízen meghatározta, milyen koordináta rendszereket, és milyen koordináta transzformációkat vizsgál. Természetesen most (a relativitás elméletben) ezek a koordináta transzformációk nem csak a tér-, hanem az idő-koordinátákat is transzformálják.

/2. Definíció: Egy koordináta rendszert inercia rendszernek nevezünk, ha benne a magukra hagyott testek (tehát akikre semmiféle erő nem hat) állandó sebességgel, egyenes vonalon mozognak (tehát az életútjuk egyenes). Mi most csak inercia rendszerekkel foglalkozunk. Bármely két inercia rendszer egyenértékű, egymáshoz képest egyenes vonalú egyenletes mozgást végeznek.
/3. Definíció: A négydimenziós téridőben két esemény négyes távolságának négyzete: Δ s 2 =c 2 Δ t 2 −Δ x 2 −Δ y 2 −Δ z 2 ahol c a fény sebessége, Δ t, Δ x, Δ y és Δ z jelöli a két esemény idő- illetve tér-koordinátáinak különbségét. Két esemény négyes távolsága ennek a négyzetgyöke, csak akkor definiáljuk, ha Δ s 2 ≥0 .
/I. Feladat: Lásd be, hogy két esemény közti négyes távolság pontosan akkor 0, ha az őket összekötő egyenes fénysebességű. Ez azt jelenti, hogy ha valaki végigéli az összekötő szakasz mentén sorakozó eseményeket, akkor az illető egész idő alatt egyenes vonalú fénysebességű mozgást végez. (Ez csak úgy lehetséges, ha az illető teljes egészében fényből, vagy valami hasonlóan abszurd anyagból áll.)
/4. Érdekesség: A négyes távolság fizikai jelentése: a két esemény közt eltelt idő annak az egyénnek a szemszögéből mérve, aki mindkét eseménynél jelen volt, és egész idő alatt egyenes vonalban, állandó sebességgel mozgott. Ez persze csak akkor értelmezhető, ha fénysebesség túllépése nélkül megvalósítható ez az utazás -- ezért van az, hogy a négyes távolságot nem minden esemény-párra definiáltuk. Ha két eseménynek nincs négyes távolsága, akkor van olyan inercia rendszer, amiből egyidejűnek tűnnek, és olyan is van, amelyikből az egyik, illetve a másik tűnik korábbinak: nem lehet konzisztens módon időrendbe tenni őket. Ha van négyes távolságuk, akkor egyetlen inercia rendszerből sem láthatók egyidejűnek, és konzisztens időrend is megadható köztük -- persze ehhez irányítanunk kell a téridőt, amit most nem részletezünk.
/II. Feladat: Lásd be, hogy a téridő egy E eseményén áthaladó fénysebességű egyenesek egy kúpot alkotnak: ezt nevezik fénykúpnak. A kúp három részre osztja a téridőt. Mi lehet ezen tartományok fizikai jelentése?
/5. Érdekesség: A négyes távolságra fordított háromszög egyenlőtlenség érvényes: Ha három eseménynek páronként van négyes távolsága, akkor az események időbeli sorrendje meghatározható. Ezek után az (időrendben) első és harmadik közti négyes távolság legalább akkora, mint az első-második távolság és a második-harmadik távolság összege, egyenlőség pedig csak akkor áll fenn, ha a három esemény egy egyenesre esik. Ezt a jelenséget hívják a fizikusok iker paradoxonnak: egyhelyben ülve öregedni mindig tovább tart, mint oda-vissza szaladgálva.
/6. Érdekesség: (Most olyan folytonos görbékkel foglalkozunk, amelyeknek mindenütt van érintője.) Egy görbe négyes hosszát akkor tudjuk definiálni, ha az érintője minden pontban legfeljebb c meredekségű -- azaz akkor, ha egy ember végigélheti a görbe mentén sorakozó eseményeket anélkül, hogy közben elérné, vagy túllépné a fénysebességet. Az ilyen görbékre mondjuk: időszerű görbe. Ha emberünk menetközben méri az eltelt időt -- a saját szemszögéből nézve -- a kapott értéket a fizikusok sajátidőnek nevezik, és ez lesz a görbe négyes hossza. Matematikai definíció: megközelítjük a görbét rövid szakaszokkal, a szakaszok négyes hosszát összeadjuk. A négyes hosszúság ennek az összegnek a határértéke lesz, ha a közelítést minden határon túl finomítjuk.
/7. Érdekesség: A fordított háromszög egyenlőtlenség -- tehát az iker paradoxon -- görbékre is átvihető. Két esemény közöt húzható összes időszerű görbék közül az egyenes szakasz négyes hossza (azaz sajátideje) a lehető legnagyobb.
/8. Definíció: A négydimenziós téridő azon bijektív transzformációi, amelyek megtartják a négyes távolság négyzetét, egy csoportot alkotnak. Ezt hívjuk Poincaré csoportnak. Az origót helyben hagyó csoport elemek egy részcsoportot alkotnak, ezt hívják Lorentz csoportnak -- szokásos jelölése O(1 ,3 ).
/9. Megjegyzés: A fenti definícióban a négyes távolság négyzete helyett írhattuk volna magát a négyes távolságot is, fizikus szemmel talán természetesebb lenne -- de így egyszerűbbek a bizonyítások. Azt sem kell feltétlenül kikötni, hogy csak bijektív transzformációkat nézünk: egyszerűen belátható, hogy a négyes távolságot megtartó transzformációk automatikusan bijektívek.
/III. Feladat: Különbözik-e egymástól a Poincaré csoport és a Lorentz csoport? Megoldások
/IV. Feladat: Bizonyítsd be, hogy a Poincaré csoport (a fenti definícióval) valóban csoport, O(1 ,3 ) valóban részcsoport. Megoldások

A fizikus magyarázatokat mellőzve elfogadjuk alapelvnek a következő tételt, mint a relativitás elmélet alapelvét:

/10. Tétel: Két esemény négyes távolságának négyzete bármelyik inercia rendszerben mérve ugyanannyi. Tehát két inercia rendszer közti koordináta transzformáció mindig a Poincaré csoport eleme.
/11. Megjegyzés: Fordítva is igaz: a Poincaré csoport minden eleme felfogható, mint inercia rendszerek közti koordináta transzformáció. Ezt nem látjuk be precízen, de a feladatokból lényegében ki fog derülni.

Az egyszerűség kedvéért (meg a rajzképességem korlátai miatt) most csak az első térbeli koordináta tengelyen zajló eseményekkel foglalkozunk:

/12. Konvenció: Mostantól két dimenziós téridőben dolgozunk. Minden eseménynek van egy idő koordinátája és egy tér koordinátája: (t,x).
/13. Definíció: A kétdimenziós téridő azon transzformációi, amelyek megtartják a négyes távolság négyzetét, egy csoportot alkotnak. Ezt úgy hívjuk, hogy Poincaré csoport 2 dimenzióban. Azok a csoport elemek, amelyek az origót helyben hagyják, egy részcsoportot alkotnak: Lorentz csoport 2 dimenzióban -- szokásos jelölése O(1 ,1 ).
/V. Feladat: Lásd be, hogy a Poincaré csoport 2 dimenzióban (a fenti definícióval) valóban csoport! Lásd be, hogy O(1 ,1 ) valóban részcsoport.

Lorentz transzformációk

A relativitás elméletben a Lorentz transzformáció írja le a két, egymáshoz képest v sebességgel mozgó koordináta rendszer közti összefüggéseket -- természetesen most az itő koordinátákat is transzformáljuk, nem csak a tér koordinátákat.

/14. Definíció: Ez egy Gif formájú film -- kár, hogy nem tudod megnézni Ha két (2 dimenziós) inercia rendszer origója ugyanaz az esemény, egymáshoz viszonyított sebességük v (amely abszolút értéke kisebb a fénysebességnél, c-nél), akkor a köztük érvényes koordináta transzformáció a Lorentz transzformáció: (x,t)→(x−vt1 −v 2 c 2 ,t−xvc 2 1 −v 2 c 2 )

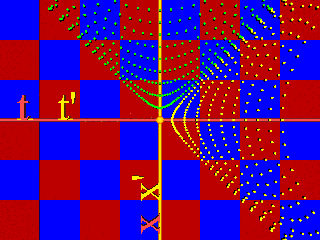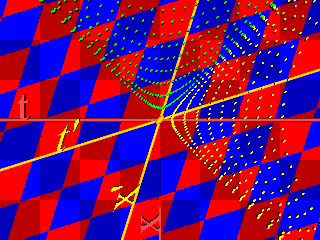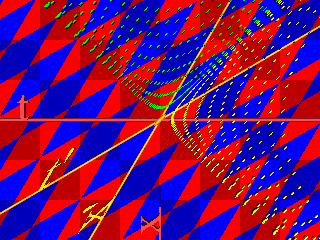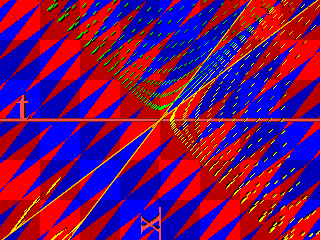
A filmen a fénysebesség: c=1 , a v sebesség 0-tól 1-ig nő. A pöttyös hiperbolák mentén a távolság-négyzet állandó: a sárgákon pozitív, a zöldeken negatív. Látható, hogy az egyes pontok pályái hiperbolák, az egyenesek viszont egyenesek maradnak (bár menet közben megnyúlnak).

/15. Konvenció: Mostantól az időt évben, a távolságot fényévben mérjük -- tehát a fénysebesség: c=1 .
/16. Megjegyzés: Mivel a fénysebességet sem elérni,sem túllépni nem lehet, azért a Lorentz transzformációt csak 1 >v>−1 sebességekre értelmezzük. Más sebességekre a nevező bajt okozna. A Lorentz transzformáció mátrix szorzás segítségével így írható: (x t)→1 1 −v 2 (1 −v −v 1 )⋅(x t)
/VI. Feladat: Lássuk be, hogy a Lorentz transzformációk megőrzik a négyes távolságot, tehát az O(1 ,1 ) csoport elemei.
/VII. Feladat: Lásd be, hogy a Lorentz transzformációk mátrixai pontosan azok az 1 determinánsú mátrixok, amelyek ilyen alakúak: (A B B A) ahol A,B valós számok, A>0 . Lásd be, hogy a fenti mátrixhoz tartozó sebesség éppen BA.
/VIII. Feladat: Lásd be, hogy a v és w sebességhez tartozó Lorentz transzformációk kompozíciója megegyezik a v+w1 +vw sebességhez tartozó Lorentz transzformációval. Ezt hívják a fizikában a sebességek addíciós tételének. Megoldások
/IX. Feladat: Lássuk be, hogy az addíciós tételben fénysebességnél kisebb v és w sebességek esetén mindig fénysebességnél kisebb eredményt kapunk.
/X. Feladat: Lássuk be, hogy a Lorentz transzformációk Abel csoportot alkotnak. Megoldások
/XI. Feladat: Mekkora a Lorentz transzformációk rendje?
/XII. Feladat: Ha ismered a hiperbolikus függvényeket: Lásd be, hogy tetszőleges α valós számra az M(α)=(chα −shα −shα chα) mátrix éppen a thα sebességű Lorentz transzformáció mátrixa. Lásd be, hogy ez egy bijekció a valós számok halmaza és a Lorentz transzformációk halmaza között. Lásd be, hogy M művelet tartó: M(α+β)=M(α)⋅M(β). Tehát a Lorentz transzformációk csoportja izomorf (lásd a 4/3. definíciót) a valós számok additív csoportjával. Megoldások
/17. Megjegyzés: Ez ad egy másik bizonyítást az addíciós tételre: azonnal következik a th függvény addíciós tételéből.
/XIII. Feladat: Lásd be, hogy egy origótól különböző pontot minden Lorentz transzformáció más-más pontba visz, és a képpontok összessége egy hiperbola egyik ága. A hiperbola egyenlete: t 2 −x 2 =állandó asszimptotái az origón áthaladó 1 meredekségű egyenesek.

A Lorentz csoport vizsgálata két dimenzióban

Ebben az alfejezetben csak feladatok lesznek, ez a rész órán nem is szerepelt.

/XIV. Feladat: Az O(1 ,1 ) csoport elemei mind mátrixszal való szorzások. Ezt be is látjuk a következő néhány felatatban. Előtte azomban lásd be, hogy pontosan az (A B B A) alakú ±1 determinánsú mátrixokkal való szorzások tartoznak O(1 ,1 )-be.
/XV. Feladat: Lásd be, hogy az O(1 ,1 ) csoport elemei egyenes tartó transzformációk: minden egyenest egyenesbe transzformálnak.
/XVI. Feladat: Lásd be, hogy az O(1 ,1 ) csoport elemei a ±1 meredekségű egyeneseket ugyanilyen meredekségű egyenesekbe képezik. Mi a helyzet más meredekségekkel?
/XVII. Feladat: Lásd be, hogy az O(1 ,1 ) csoport elemei saját magukba képezik azokat a hiperbolákat, amelyeknek az egyenlete t 2 −x 2 =állandó Megoldások
/XVIII. Feladat: Lásd be, hogy az O(1 ,1 ) csoportnak pontosan két olyan eleme van, amelyik a (0 ,1 ) pontot helyben hagyja: az identitás, és a tér-tükrözés: (x,t)→(−x,t)
/XIX. Feladat: Lásd be, hogy az O(1 ,1 ) csoportnak pontosan két olyan eleme van, amelyik az (1 ,0 ) pontot helyben hagyja: az identitás, és az idő-tükrözés: (x,t)→(x,−t)
/XX. Feladat: Lásd be, hogy a téridő bármelyik origótól különböző pontját az O(1 ,1 ) csoportnak pontosan két eleme hagyja helyben.
/XXI. Feladat: Jelölje T:(x,t)→(x,−t) az idő-tükrözést, és X:(x,t)→(−x,t) a tér-tükrözést. Lásd be, hogy az O(1 ,1 ) csoport minden eleme egyértelműen írható fel L, LT, LX vagy LXT alakban, ahol L egy lorentz transzformáció.
/XXII. Feladat: Melyek az O(1 ,1 ) csoport végesrendű elemei? Mennyi a rendüjk?
/XXIII. Feladat: Határozd meg az O(1 ,1 ) csoport véges részcsoportjait.
/XXIV. Feladat: Lásd be, hogy a 2 dimenzióbeli Lorentz csoport minden eleme egyértelműen írható fel egy eltolás, és egy O(1 ,1 )-beli transzformáció szorzataként.